Here, you will learn Different Types of Parabola and Standard equations of parabola, focal chord, double ordinate and latus rectum of parabola.
Let’s begin –
What is Parabola ?
A parabola is the locus of a point which moves in a plane, such that its distance from a fixed point(focus) is equal to its perpendicular distance from a fixed straight line(directrix).
The Standard equation of parabola is \(y^2 = 4ax\) and it is shown in figure. For this parabola :
(i) Vertex is (0,0).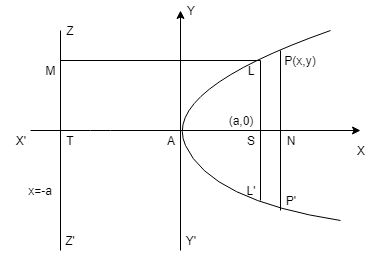
(ii) focus is (a,0)
(iii) Axis is y = 0
(iv) Directrix is x + a = 0
(a) Focal distance :
The distance of a point on the parabola from the focus is called the focal distance of the point.
(b) Focal chord :
A chord of the parabola, which passes through the focus is called a focal chord.
(c) Double ordinate :
A chord of the parabola perpendicular to the axis of the symmetry is called double ordinate.
(d) Latus rectum :
A double ordinate passing through the focus or a focal chord perpendicular to the axis of parabola is called latus rectum.
For \(y^2 = 4ax\).
Length of the latus rectum = 4a
Length of the semi latus rectum = 2a
Ends of the latus rectum are L(a, 2a) & L'(a, -2a).
Note :
(i) Perpendicular distance from focus on the directrix = half the latus rectum.
(ii) Vertex is middle point of the focus & point of intersection of directrix & axis.
(iii) Two parabolas are said to be equal if they have the same latus rectum.
Different Types of Parabola & Standard Equations of Parabola
Four different types of parabola equations are
\(y^2\) = 4ax ; \(y^2\) = -4ax ; \(x^2\) = 4ay ; \(x^2\) = -4ay.
One I had shown above and three others are shown below.
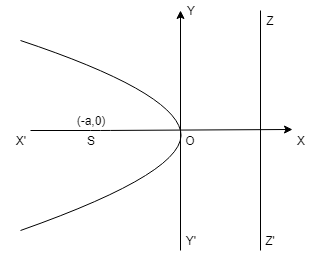
\(y^2\) = -4ax
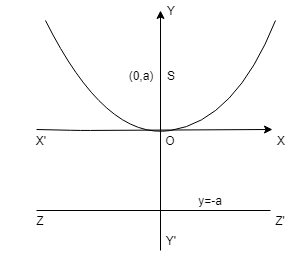
\(x^2\) = 4ay
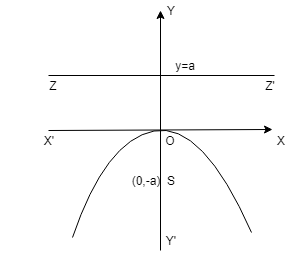
\(x^2\) = -4ay
| Parabola | Vertex | Focus | Axis | Directrix |
|---|---|---|---|---|
| \(y^2\) = 4ax | (0,0) | (a,0) | y = 0 | x = -a |
| \(y^2\) = -4ax | (0,0) | (-a,0) | y = 0 | x = a |
| \(x^2\) = +4ay | (0,0) | (0,a) | x = 0 | y = -a |
| \(x^2\) = -4ay | (0,0) | (0,-a) | x = 0 | y = a |
| \((y-k)^2\) = 4a(x-h) | (h,k) | (h+a,k) | y = k | x+a-h = 0 |
| \((x-p)^2\) = 4b(y-q) | (p,q) | (p,b+q) | x = p | y+b-q = 0 |
| Length of Latus rectum | Ends of Latus rectum | Parametric equation | Focal length |
|---|---|---|---|
| 4a | (a,\(\pm\)2a) | (a\(t^2\), 2at) | x + a |
| 4a | (-a,\(\pm\)2a) | (-a\(t^2\), 2at) | x – a |
| 4a | (\(\pm\)2a,a) | (2at, a\(t^2\)) | y + a |
| 4a | (\(\pm\)2a,-a) | (2at, -a\(t^2\)) | y – a |
| 4a | (h+a, k\(\pm\)2a) | (h+a\(t^2\), k+2at) | x – h + a |
| 4b | (p\(\pm\)2a, q+a) | (p+2at, q+a\(t^2\)) | y – q + b |
Example : Find the vertex, axis, directrix, focus, latus rectum and the tangent at vertex for the parabola \(9y^2 – 16x – 12y – 57\) = 0.
Solution : The given equation can be written as \(({y-2\over 3})^2\) =
\(16\over 9\)\(({x + 61\over 16})\) which is of the form \(y^2\) = 4ax. Hence the vertex is (-\(61\over 16\), \(2\over 3\))
The axis is y – \(2\over 3\) = 0 \(\implies\) y = \(2\over 3\)
The directrix is x + a – h = 0 \(\implies\) x + \(61\over 16\) + \(4\over 9\) \(\implies\) x = \(-613\over 144\)
The focus is (h+a, k) \(\implies\) (\(-485\over 144\), \(2\over 3\))
Length of the latus rectum = 4a = \(16\over 9\)
The tangent at the vertex is x – h = 0 \(\implies\) x = \(-61\over 16\)
Position of a point relative to a parabola :
The point (\(x_1\),\(y_1\)) lies outside, on or inside the parabola \(y^2\) = 4a\(x_1\) is positive, zero or negative.
Related Questions
Find the value of k for which the point (k-1, k) lies inside the parabola \(y^2\) = 4x.
The focal distance of a point on the parabola \(y^2\) = 12x is 4. Find the abscissa of this point.
The slope of the line touching both the parabolas \(y^2\) = 4x and \(x^2\) = -32 is
