Formula for Length of Arc of Circle with Examples

Here you will learn what is the formula for length of arc of circle with examples based on it.

Let’s begin –

What is an Arc ?

Arc is a piece of circle. In the figure AB is an arc.

The area OAB in the figure is called sector of the circle.

Formula for Length of Arc of Circle

Let an arc AB make an angle $\theta$ < 180 at the centre of circle of radius r.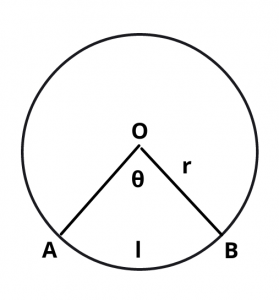

Then,

Length of the arc = $2\pi r \theta\over 360$

i.e. $l$ =  $\pi r \theta\over 180$

Also Read : Area of a Ring – Formula and Examples

Example : A sector is cut from a circle of radius 42 cm. The angle of the sector is 120. Find the length of its arc.

Solution : Here r = 42 cm and $\theta$ = 120

Length of arc of sector of angle $\theta$ and radius r = $l$ = $\pi r \theta\over 180$

$\implies$   $l$ = $120\over 180$ $\times$ $22\over 7$ $\times$ 42 = 88 cm

Hence, length of arc is 88 cm.

Example : A pendulum swings through an angle 60 and describes an arc 8.8 cm in length. Find the length of the pendulum.

Solution : Here, length of arc ($l$) = 8.8 cm and $\theta$ = 60

Length of arc of sector of angle $\theta$ and radius r = $l$ = $\pi r \theta\over 180$

$\implies$   8.8 = $60\over 180$ $\times$ $22\over 7$ $\times$ r

$\implies$  r = $8.8 \times 180 \times 7\over 60 \times 22$

$\implies$ r = $4.4 \times 3 \times 7\over 11$  cm = 8.4 cm

Hence, length of pendulum is 88 cm.