Sector of a Circle Area and Perimeter – Formula and Examples

Here you will learn perimeter and area of sector of circle formula with examples.

Let’s begin –

What is Sector of a Circle ?

The region bounded by two radii of a circle and the arc intercepted by them is called a sector of the circle.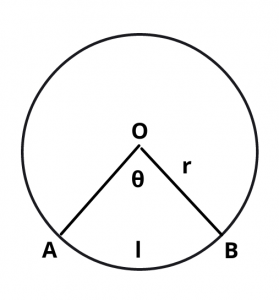

A sector is measured by the angle which its arc subtends at the centre of the circle.

Also Read : Formula for Length of Arc of Circle with Examples

Perimeter = 2r + $\pi r \theta\over 180$

Area = $\theta\over 360$ $\times$ $\pi r^2$ = $\pi r^2 \theta\over 360$

When length of the arc ( $l$ ) is given, then area of sector

Area = $1\over 2$ $lr$

Example : A sector is cut from a circle of diameter 21 cm. If the angle of the sector is 150, find its area.

Solution : We have,

Diameter = 21 cm $\implies$ radius = $21\over 2$ cm

Angle of sector = 150

Area of the sector = $\theta\over 360$ $\times$ $\pi r^2$ = $150\over 360$ $\times$ $22\over 7$ $\times$ $({21\over 2})^2$

= $5\over 12$ $\times$ $22\over 7$ $\times$ $21\over 2$ $\times$ $21\over 2$ = $5\times 11\times 21\over 4\times 2$ = 144.38 $cm^2$

Hence, the area of sector is 144.38 $cm^2$

Example : The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.

Solution : Let O be the centre with radius 5.6 cm, and let OAB be its sector(as shown in figure above) with perimeter 27.2 cm

Then, OA + OB + arc AB = 27.2 cm

$\implies$ 5.6 + 5.6 + arc AB = 27.2 cm

$\implies$ arc AB = 16 cm

Area of the sector OAB = $1\over 2$ $\times$ radius $\times$ arc length

= $1\over 2$ $\times$ 5.6 $\times$ 16 = 44.8 $cm^2$

Hence, the area of sector is 44.8 $cm^2$