Segment of a Circle Area – Formula and Examples

Here you will learn what is the formula for major and minor segment of a circle to find its area with examples.

Let’s begin –

What is the Segment of a Circle ?

A segment of a circle is defined as the part of circle bounded by a chord and the arc.

In the figure, the part APB is a segment of circle.

Area of Segments Formula

Let AB be a chord of circle with radius r. Let $\angle$ AOB = $\theta$ and 0 < $\theta$ 180.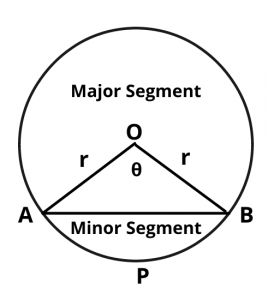

The minor segment corresponding to chord AB is shown in figure.

Area of Minor Segment = Area of sector OAB – Area of triangle OAB

Since area of sector = $\theta\over 360$ $\pi r^2$ and 

area of triangle = $1\over 2$ $r^2 sin\theta$

Hence, Area of Minor Segment = $\theta\over 360$ $\pi r^2$ – $1\over 2$ $r^2 sin\theta$

Area of Major Segment = Area of Circle – Area of Minor Segment

Hence, Area of Major Segment = $\pi r^2$ – ( $\theta\over 360$ $\pi r^2$ – $1\over 2$ $r^2 sin\theta$)

Example : A chord 10 cm long is drawn in a circle whose radius is $\sqrt{50}$ cm. Find the area of segments.

Solution : Radius of the circle = $\sqrt{50}$ cm

$\therefore$   Area of circle = $22\over 7$ $\times$ $(\sqrt{50})^2$ = $1100\over 7$ = 157.14 $cm^2$

Since, OA = OB = $\sqrt{50}$ cm

$(OA)^2$ + $(OB)^2$ = 50 + 50 = 100 cm

$(AB)^2$ = 100

$\therefore$  $(OA)^2$ + $(OB)^2$ = $(AB)^2$  $\implies$  $\angle$ AOB = 90

Area of sector OAB = $90\over 360$ $\times$ $22\over 7$ $\times$  $(\sqrt{50})^2$ = 39.29 $cm^2$

Area of triangle OAB = $1\over 2$ $r^2 sin\theta$ = $1\over 2$ $\times$ (50 sin 90) = 25 $cm^2$

$\therefore$  Area of Minor Segment = Area of sector OAB – Area of triangle OAB

= 39.29 – 25 = 14.29  $cm^2$

Area of Major Segment = Area of Circle – Area of Minor Segment

= 157.14 – 14.29 = 142.85 $cm^2$