A parabola is locus of a point which moves in a plane, such that its distance from a fixed point called focus is equal to its perpendicular distance from a fixed straight line called directrix. Graph of a Parabola and their types are shown below.
Basic Concepts of a Parabola
(a) Focal distance : The distance of a point on parabola from the focus is called focal distance of the point.
(b) Focal chord : A chord of parabola, which passes through focus is called focal chord.
(c) Double ordinate : A chord of the parabola perpendicular to the axis of the symmetry is called double ordinate.
(d) Latus rectum : A double ordinate passing through focus or a focal chord perpendicular to axis of parabola is called latus rectum.
Types and Graph of a Parabola :
Four standard forms of parabola are \(y^2\) = 4ax ; \(y^2\) = -4ax ; \(x^2\) = 4ay ; \(x^2\) = -4ay. All of them with their graphs are given below :
(i) Parabola \(y^2 = 4ax\) : 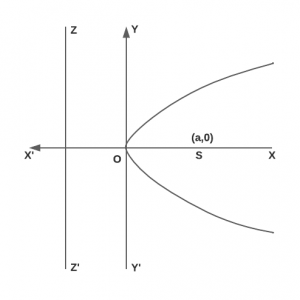
Vertex O is (0, 0)
Focus S is (a, 0)
Axis is y = 0
Directrix ZZ’ is x = -a
Focal length = x + a
Length of Latus rectum = 4a
(ii) Parabola \(y^2 = -4ax\) :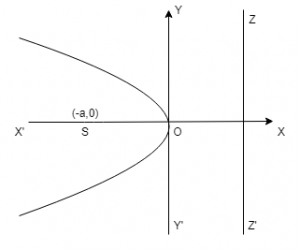
Vertex O is (0,0)
Focus S is (-a,0)
Axis is y = 0
Directrix ZZ’ is x = a
Focal length = x – a
Length of Latus rectum = 4a
(iii) Parabola \(x^2 = 4ay\) :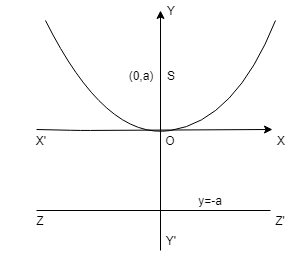
Vertex O is (0,0)
Focus S is (0,a)
Axis is x = 0
Directrix ZZ’ is y = -a
Focal length = y + a
Length of Latus rectum = 4a
(iv) Parabola \(x^2 = -4ay\) :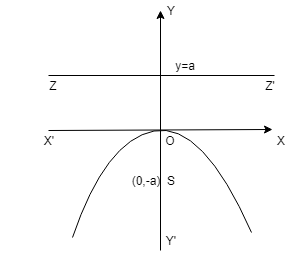
Vertex O is (0,0)
Focus S is (0,-a)
Axis is x = 0
Directrix ZZ’ is y = a
Focal length = y – a
Length of Latus rectum = 4a
Hope you learnt basic concepts and graph of a parabola, learn more concepts of parabola and practice more questions to get ahead in the competition. Good luck!
