Solution :
We have : DB = 3CD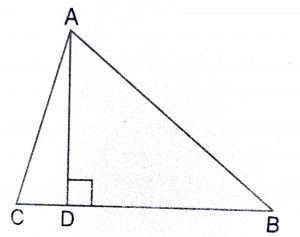
Now, BC = DB + CD
i.e. BC = 3CD + CD [because BD = 3CD]
BC = 4CD
\(\therefore\) CD = \(1\over 4\) BC and DB = 3CD = \(3\over 4\) BC ……….(1)
Since triangle ABD is a right triangle, right angled at D, therefore, by Pythagoras Theorem, we have :
\({AB}^2\) = \({AD}^2\) + \({DB}^2\) ……….(2)
In triangle ACD,
\(\angle\) D = 90 , \({AC}^2\) = \({AD}^2\) + \({CD}^2\) ……..(3)
Subtracting (3) from (2), we get
\({AB}^2\) – \({AC}^2\) = \({DB}^2\) – \({CD}^2\)
\({AB}^2\) – \({AC}^2\) = \(({3\over 4}BC)^2\) – \(({1\over 4}BC)^2\) (using (1))
\({AB}^2\) – \({AC}^2\) = \(({9\over 16} – {1\over 16})\)\({BC}^2\)
\({AB}^2\) – \({AC}^2\) = \({1\over 2}\)\({BC}^2\)
\(\implies\) \(2{AB}^2\) = \(2{AC}^2\) + \({BC}^2\)
