D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that \({AE}^2\) + \({BC}^2\) = \({AB}^2\) + \({DE}^2\).

Solution :

From triangle ACE,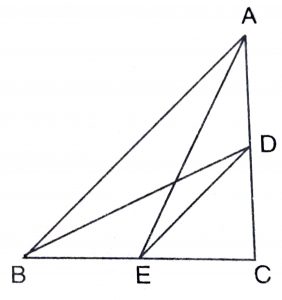

\({AE}^2\) = \({EC}^2\) + \({AC}^2\)       ……….(1)          (By Pythagoras Theorem)

From triangle DCB,

\({BD}^2\) = \({BC}^2\) + \({DC}^2\)        ………(2)

Adding (1) and (2), we get

\({AE}^2\) + \({BD}^2\) = \({EC}^2\) + \({AC}^2\) + \({BC}^2\) + \({DC}^2\)

By Pythagoras Theorem in right triangle ECD and ABC, \({DE}^2\) = \({EC}^2\) + \({DC}^2\)  and  \({AB}^2\) = \({BC}^2\) + \({AC}^2\)

Hence,  \({AE}^2\) + \({BC}^2\) = \({AB}^2\) + \({DE}^2\)