Solution :
Let ABC be an equilateral triangle and let D be a point on BC such that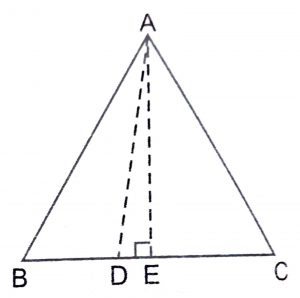
BD = \(1\over 3\) BC.
Draw AE \(\perp\) BC. Join AD.
In \(\triangle\) AEB and AEC, we have :
AB = AC (ABC is equilateral)
\(\angle\) AEB = \(\angle\) AEC
and AE = AE
\(\therefore\) By SAS criteria of congruence, we have :
\(\triangle\) AEB \(\cong\) \(\triangle\) AEC
So, BE = EC
Now, we have :
BD = \(1\over 3\)BC, DC = \(2\over 3\)BC and BE = EC = \(1\over 2\)BC ……….(1)
Since, \(\angle\) C = 60, therefore
\(\triangle\) ADC is an acute triangle.
\(\therefore\) \({AD}^2\) = \({AC}^2\) + \({DC}^2\) – \(2DC \times EC\)
= \({AC}^2\) + \(({2\over 3}BC)^2\) – \(2\times {2\over 3}BC\times {1\over 2}BC\)
= \({AC}^2\) + \(({4\over 9}BC)^2\) – \(({2\over 3}BC)^2\)
= \({AB}^2\) + \(({4\over 9}AB)^2\) – \(({2\over 3}AB)^2\) (AB = AB = AC)
= \((9 – 4 – 6){AB}^2\over 9\) = \({7\over 9}{AB}^2\)
So, \(9{AD}^2\) = \(7{AB}^2\)
