Solution :
Let ABC be and equilateral triangle and let AD \(\perp\) BC.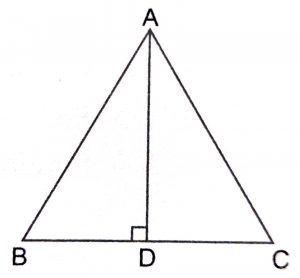
In \(\triangle\) ADB and ADC, we have :
AB = AC (given)
AD = AD (common side of triangle)
and \(\angle\) ADB = \(\angle\) ADB (each 90)
By RHS criteria of congruence, we have :
\(\triangle\) ADB \(\cong\) \(\triangle\) ADC
So, BD = DC or BD = DC = \(1\over 2\) BC ……..(1)
Since \(\triangle\) ADB is a right triangle, angled at D, by Pythagoras theorem, we have :
\({AB}^2\) = \({AD}^2\) + \({BD}^2\)
\({AB}^2\) = \({AD}^2\) + \(({1\over 2}BC)^2\) (from 1)
\({AB}^2\) = \({AD}^2\) + \({1\over 4}{BC}^2\)
\({AB}^2\) = \({AD}^2\) + \({AB}^2\over 4\) (\(\therefore\) BC = AB)
\({3\over 4}{AB}^2\) = \({AD}^2\) or \(3{AB}^2\) = \(4{AD}^2\)
