Solution :
Given : \(\triangle\) ABC ~ \(\triangle\) DEF and AP, DQ are their medians.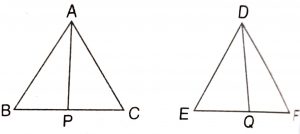
To Prove : \(area(\triangle ABC)\over area(\triangle DEF)\) = \({AP}^2\over {DQ}^2\)
Proof : Since the ratio of the area of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
\(\therefore\) \(area (\triangle ABC)\over area (\triangle DEF)\) = \({AB}^2\over {DE}^2\) ………..(1)
Now, \(\triangle\) ABC ~ \(\triangle\) DEF
\(\implies\) \(AB\over DE\) = \(BC\over EF\) = \(2BP\over 2EQ\) = \(BP\over EQ\) ………….(2)
Thus, \(AB\over DE\) = \(BP\over EQ\) and \(\angle\) B = \(\angle\) E (because \(\triangle\) ABC ~ \(\triangle\) DEF)
By SAS similarity,
\(\triangle\) APB ~ \(\triangle\) DQE
So, \(BP\over EQ\) = \(AP\over DQ\) ……….(3)
From (2) and (3), we get
\(AB\over DE\) = \(AP\over DQ\) \(\implies\) \({AB}^2\over {DE}^2\) = \({AP}^2\over {DQ}^2\) ………(4)
Substituting the value of \({AB}^2\over {DE}^2\) from (4) in (1), we get
\(area (\triangle ABC)\over area (\triangle DEF)\) = \({AP}^2\over {DQ}^2\)
