Solution :
Given : A square ABCD, equilateral triangles BCE and ACF have been drawn on side BC and the diagonal AC respectively.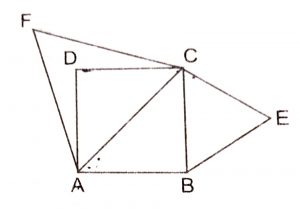
To Prove : \(area(\triangle BCE)\) = \(1\over 2\)\(area(\triangle DEF)\)
Proof : Since all equilateral triangles are similar.
\(\implies\) \(\triangle\) BCE ~ \(\triangle\) ACF
\(area(\triangle BCE)\over area(\triangle ACF)\) = \({BC}^2\over {AC}^2\)
Since, Diagonal = \(\sqrt{2}\) side, So, AC = \(\sqrt{2}\) BC
\(\implies\) \(area(\triangle BCE)\over area(\triangle ACF)\) = \({BC}^2\over {\sqrt{2} BC}^2\)
\(\implies\) \(area(\triangle BCE)\over area(\triangle ACF)\) = \(1\over 2\)
