Tick the correct answer and justify : ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is (a) 2 : 1 (b) 1 : 2 (c) 4 : 1 (d) 1 : 4

Solution :

Since \(\triangle\) ABC and BDE are equilateral triangles, they are equiangular and hence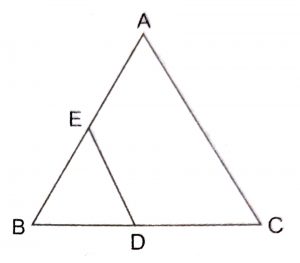

\(\triangle\) ABC ~ \(\triangle\) BDE

So, \(area(\triangle ABC)\over area(\triangle BDE)\) = \({BC}^2\over {BD}^2\)

or  \(area(\triangle ABC)\over area(\triangle BDE)\) = \({2BD}^2\over {AC}^2\)

\(\implies\)  \(area(\triangle ABC)\over area(\triangle BDE)\) = \(4\over 1\)

\(\therefore\) (d) is the correct answer.