Solution :
Since D and E are the mid-points of the sides BC and CA respectively of \(\triangle\) ABC.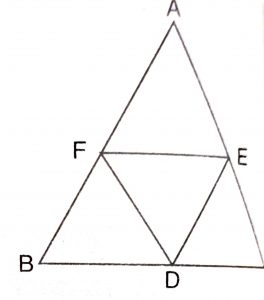
\(\therefore\) DE || BA
\(\implies\) DE || FA ……….(1)
Since D and F are the mid-points of the sides BC and AB respectively of \(\triangle\) ABC. Therefore,
DF || CA \(\implies\) DF || AE ………..(2)
From (1) and (2), we get AFDE is a parallelogram
Similarly, BDEF is a parallelogram.
In triangle DEF and ABC,
\(\angle\) FDE = \(\angle\) A (opposite angles of ||gm AFDE)
\(\angle\) DEF = \(\angle\) B (opposite angles of ||gm BDEF)
\(\therefore\) By AA similarity,
\(\triangle\) DEF ~ \(\triangle\) ABC
\(\implies\) \(area(\triangle DEF)\over area(\triangle ABC)\) = \({DE}^2\over {AB}^2\) = \(1\over 4\)
(The areas of two similar triangles are in the ratio of the squares of the corresponding sides)
Hence, Area of triangle DEF : Area of triangle ABC = 1 : 4
