
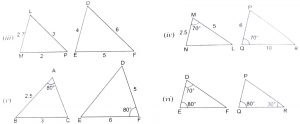
Solution :
(i) In triangles ABC and PQR, we observe that
\(\angle\) A = \(\angle\) B = 60,
\(\angle\) P = \(\angle\) Q = 80
and \(\angle\) C = \(\angle\) R = 40
\(\therefore\) By AAA criterion of similarity, \(\triangle\) ABC ~ \(\triangle\) PQR
(ii) In triangles ABC and PQR, we observe that
\(AB\over QR\) = \(BC\over RP\) = \(CA\over PQ\) = \(1\over 2\)
\(\therefore\) By SSS criterion of similarity, \(\triangle\) ABC ~ \(\triangle\) PQR
(iii) In triangles LMP and DEF, we observe that the ratio of the sides of these triangles are not equal.
So, the two triangles are not similar.
(iv) In triangles MNL and QPR, we observe that \(\angle\) M = \(\angle\) Q = 70
But, \(MN\over PQ\) \(\ne\) \(ML\over PR\)
So, these two triangles are not similar as they do not satisfy the SAS criterion for similarity.
(v) In triangles ABC and FDE, we observe that \(\angle\) A = \(\angle\) F = 80
But, \(AB\over DE\) \(\ne\) \(AC\over DF\)
So, these two triangles are not similar as they do not satisfy the SAS criterion for similarity.
(vi) In triangles DEF and PQR, we observe that
\(\angle\) D = \(\angle\) P = 70,
\(\angle\) E = \(\angle\) Q = 80
\(\therefore\) By AAA criterion of similarity, \(\triangle\) DEF ~ \(\triangle\) PQR
