Solution :
Given : A quadrilateral ABCD, in which the diagonals AC and BD intersect each other at O such that 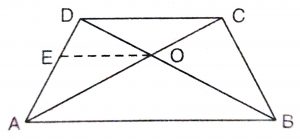 \(AO\over BO\) = \(CO\over DO\).
\(AO\over BO\) = \(CO\over DO\).
To Prove : ABCD is a trapezium.
Construction : Draw EO || BA, meeting AD in E.
Proof : In triangle ABD, EO || BA
By basic proportionality theorem,
\(DE\over EA\) = \(DO\over OB\) …………(1)
But Given that, \(AO\over BO\) = \(CO\over DO\) \(\implies\) \(DO\over BO\) = \(CO\over AO\) …………..(2)
From (1) and (2), we get
\(DE\over EA\) = \(CO\over OA\)
By converse of basic proportionality theorem,
\(\implies\) EO || DC
But by construction, EO || BA
\(\therefore\) DC || BA
Hence, ABCD is a trapezium.
