Solution :
Since BD is a line and OC is a ray on it.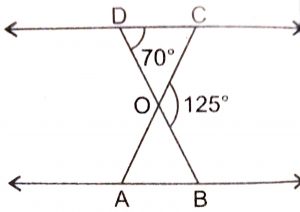
\(\angle\) DOC + \(\angle\) BOC = 180
So, \(\angle\) DOC + 125 = 180
\(\angle\) DOC = 55
In triangle CDO, we have :
\(\angle\) CDO + \(\angle\) DOC + \(\angle\) DCO = 180
70 + 55 + \(\angle\) DCO = 180
\(\angle\) DCO = 55
Given that \(\triangle\) ODC ~ \(\triangle\) OBA
\(\angle\) ODC = \(\angle\) OBA, \(\angle\) OCD = \(\angle\) OAB
\(\angle\) OBA = 70 and \(\angle\) OAB = 55
Hence, \(\angle\) DOC = 55, \(\angle\) DCO = 55 and \(\angle\) OAB = 55
