Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(OA\over OC\) = \(OB\over OD\).

Solution :

Given : A trapezium ABC whose diagonals AC and BD intersect each other at O and AB || DC.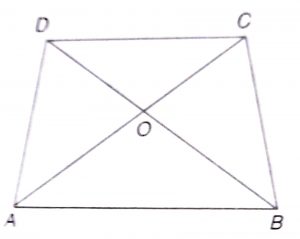

To Prove : \(OA\over OC\) = \(OB\over OD\)

Proof : In triangle DOC and AOB,

AB || DC and AC is transversal, then

\(\angle\) DCO = \(\angle\) OAB                     (Alternate angles)

\(\angle\) ODC = \(\angle\) OBA                    (Alternate angles)

\(\angle\) DOC = \(\angle\) AOB                       (vertically opposite angles)

Hence, By AAA similarity,

\(\triangle\) DOC ~ \(\triangle\) BOA

\(\implies\)    \(OA\over OC\) = \(OB\over OD\)