In the figure, \(QR\over QS\) = \(QT\over PR\) and \(\angle\) 1 = \(\angle\) 2. Show that \(\triangle\) PQS ~ \(\triangle\) TQR.

Solution :

Given, 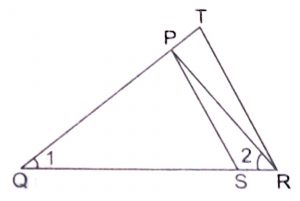 \(QR\over QS\) = \(QT\over PR\)

So, \(QT\over QR\) = \(PR\over QS\)               ……….(1)

Also given,  \(\angle\) 1 = \(\angle\) 2

Since, sides opposite to equal \(\angle\)s are equal,

So , PR = PQ              ………(2)

From (1) and (2), we get

\(QT\over QR\) = \(PQ\over QS\)      or    \(PQ\over QT\) = \(QS\over QR\)

In \(\triangle\)s PQS and TQR, we have :

\(PQ\over QT\) = \(QS\over QR\)     and    \(\angle\) PQS = \(\angle\) TQR  = \(\angle\) Q

Hence, By SAS criterion of similarity, \(\triangle\) PQS ~ \(\triangle\) TQR