S and T are points on sides PR and QR of triangle PQR such that \(\angle\) P = \(\angle\) RTS. Show that \(\triangle\) RPQ ~ \(\triangle\) RTS.

Solution :

Given : 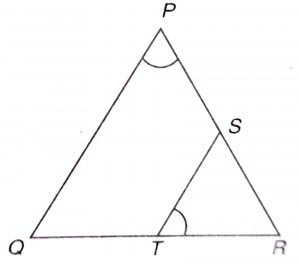\(\triangle\) RPQ and \(\triangle\) RTS where \(\angle\) P = \(\angle\) RTS

To prove : \(\triangle\) RPQ ~ \(\triangle\) RTS

Proof : In \(\triangle\) RPQ and \(\triangle\) RTS

Given,    \(\angle\) P = \(\angle\) RTS

\(\angle\) R = \(\angle\) R                (common)

Hence, By AA similarity, \(\triangle\) RPQ ~ \(\triangle\) RTS