Solution :
It is given that 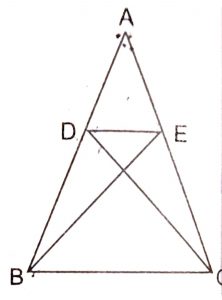 \(\triangle\) ABE \(\cong\) \(\triangle\) ACD
\(\triangle\) ABE \(\cong\) \(\triangle\) ACD
\(\therefore\) AB = AC
and AE = AD
[ because corresponding parts of congruent triangles are equal ]
So, \(AB\over AD\) = \(AC\over AE\) or \(AB\over AC\) = \(AD\over AE\) ………(1)
\(\therefore\) In triangles ADE and ABC, we have :
\(AB\over AC\) = \(AD\over AE\)
and \(\angle\) BAC = \(\angle\) DAE
Thus, by SAS criterion of similarity, \(\triangle\) ADE ~ \(\triangle\) ABC.
