Solution :
(i) In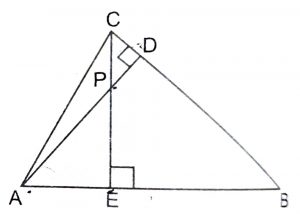 
\(\triangle\) AEP and CDP, we have
\(\angle\) AEP = \(\angle\) CDP = 90
\(\angle\) APE = \(\angle\) CPD (vertically opposite angles)
\(\therefore\) By AA similarity, we have :
\(\triangle\) AEP ~ \(\triangle\) CDP
(ii) In \(\triangle\) ABD and CBE, we have
\(\angle\) ABD = \(\angle\) CBE (common angle)
\(\angle\) ADB = \(\angle\) CEB = 90
\(\therefore\) By AA similarity, we have :
\(\triangle\) ABD ~ \(\triangle\) CBE
(iii) In \(\triangle\) AEP and ADB, we have
\(\angle\) AEP = \(\angle\) ADB = 90
\(\angle\) PAE = \(\angle\) DAB (common angles)
\(\therefore\) By AA similarity, we have :
\(\triangle\) AEP ~ \(\triangle\) ADB
(iv) In \(\triangle\) PDC and BEC, we have
\(\angle\) PDC = \(\angle\) BEC = 90
\(\angle\) PCD = \(\angle\) ECB (common angles)
\(\therefore\) By AA similarity, we have :
\(\triangle\) PDC ~ \(\triangle\) BEC
