Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that \(\triangle\) ABC ~ \(\triangle\) PQR.

Solution :

Given : 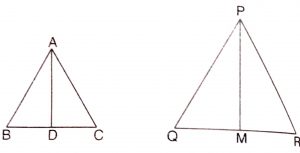\(\triangle\) ABC and \(\triangle\) PQR in which AD and PM are the medians, such that

\(AB\over PQ\) = \(BC\over QR\) = \(AD\over PM\)

To prove :  \(\triangle\) ABC ~ \(\triangle\) PQR

Proof : \(AB\over PQ\) = \(BC\over QR\) = \(AD\over PM\)

\(\implies\)  \(AB\over PQ\) = \({1\over 2}BC\over {1\over 2}QR\) = \(AD\over PM\)

\(\implies\) \(AB\over PQ\) = \(BD\over QM\) = \(AD\over PM\)

By SSS similarity,

\(\triangle\) ABD ~ \(\triangle\) PQM

\(\implies\) \(\angle\) B = \(\angle\) Q

Now, in triangle ABC and PQR, we have

\(AB\over PQ\) = \(BC\over QR\)         (given)

and  \(\angle\) B = \(\angle\) Q

So, By SAS similarity,

\(\triangle\) ABC ~ \(\triangle\) PQR