In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB \(\perp\) AC, prove that \(\triangle\) ABD ~ \(\triangle\) ECF.

Solution :

Here, \(\triangle\) ABC is an isosceles with AB = AC.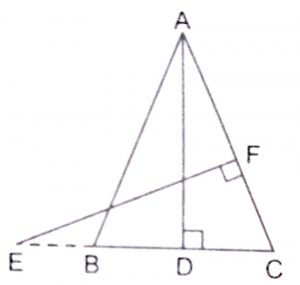

\(\therefore\)  \(\angle\) B = \(\angle\) C

In \(\triangle\)s ABD and ECF, we have

\(\angle\) ABD = \(\angle\) ECF        [\(\because\) \(\angle\) B = \(\angle\) C]

\(\angle\) ADB = \(\angle\) EFC = 90

\(\therefore\)  By AA similarity,

\(\triangle\) ABD ~ \(\triangle\) ECF