Solution :
Given : 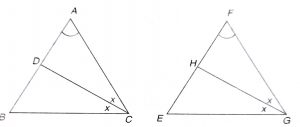 \(\triangle\) ABC ~ \(\triangle\) FEG and CD and GH are bisectors of \(\angle\) C and \(\angle\) G respectively.
\(\triangle\) ABC ~ \(\triangle\) FEG and CD and GH are bisectors of \(\angle\) C and \(\angle\) G respectively.
(i) In triangle ACD and FGH
\(\angle\) A = \(\angle\) F (\(\triangle\) ABC ~ \(\triangle\) FEG)
Since it is given that CD bisects \(\angle\) C and GH bisects \(\angle\) G and \(\angle\) C = \(\angle\) G,
\(\implies\) \(\angle\) ACD = \(\angle\) FGH
\(\therefore\) By AA similarity,
\(\triangle\) ACD ~ \(\triangle\) FGH
\(\implies\) \(CD\over GH\) = \(AC\over FG\)
(ii) In triangle DCB and HGE,
\(\angle\) B = \(\angle\) E (\(\triangle\) ABC ~ \(\triangle\) FGH)
Since it is given that CD bisects \(\angle\) C and GH bisects \(\angle\) G and \(\angle\) C = \(\angle\) G,
\(\implies\) \(\angle\) DCB = \(\angle\) HGE
\(\therefore\) By AA similarity,
\(\triangle\) DCB ~ \(\triangle\) HGE
(iii) In triangle DCA and HGF
\(\angle\) A = \(\angle\) F (\(\triangle\) ABC ~ \(\triangle\) FEG)
Since it is given that CD bisects \(\angle\) C and GH bisects \(\angle\) G and \(\angle\) C = \(\angle\) G,
\(\implies\) \(\angle\) DCA = \(\angle\) HGF
\(\therefore\) By AA similarity,
\(\triangle\) DCA ~ \(\triangle\) HGF
