In the figure, ABC and AMP are two right triangles, right angled at B and M respectively, Prove that (i) \(\triangle\) ABC ~ \(\triangle\) AMP (ii) \(CA\over PA\) = \(BC\over MP\)

Solution :

(i)  In triangles, ABC and AMP, we have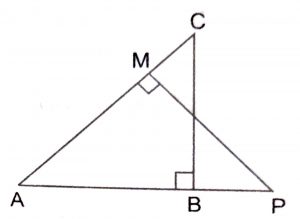

\(\angle\) ABC = \(\angle\) AMP = 90       (given)

\(\angle\)  BAC = \(\angle\) MAP          (common angles)

\(\therefore\)  By AA similarity, we have

\(\triangle\) ABC ~ \(\triangle\) AMP

(ii)  We have :

\(\triangle\) ABC ~ \(\triangle\) AMP          (as proved above)

So, In similar triangles, corresponding sides are proportional.

\(\implies\)   \(CA\over PA\) = \(BC\over MP\)