Solution :
Given : D is a point on the side BC of a triangle ABC, such that \(\angle\) ADC = \(\angle\) BAC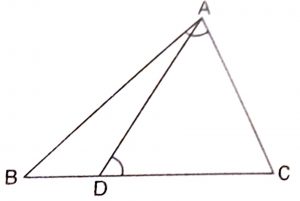
To Prove : \({CA}^2\) = \(DC \times CB\)
Proof : In triangles ABC and DAC,
\(\angle\) BAC = \(\angle\) ADC (given)
\(\angle\) C = \(\angle\) C (common)
\(\angle\) ABC = \(\angle\) DAC (third angles of the triangles)
\(\therefore\) \(\triangle\)s ABC and DAC are equiangular and hence, similar
\(\therefore\) \(BC\over AC\) = \(AC\over DC\)
\(\implies\) \({CA}^2\) = \(DC \times CB\)
