Solution :
Given : Two triangles ABC and DEF, in which AP and DQ are the medians, such that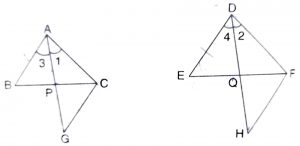
\(AB\over DE\) = \(AC\over DF\) = \(AP\over DQ\)
To prove : \(\triangle\) ABC ~ \(\triangle\) DEF
Construction : Produce line AP to G, so that PG = AP. Join CG. And Produce line DQ to H, so that QH = DQ. Join FH.
Proof : In triangles APB and GPC, BP = CP (because AP is the median)
AP = GP (by construction)
and \(\angle\) APB = \\(\angle\) CPG (vertically opposite angles)
\(\therefore\) By SAS theorem of congruence,
\(\triangle\) APB \(\cong\) \(\triangle\) GPC
\(\implies\) AB = GC …….(1) (C.P.C.T)
Again, in triangles DQE and HQF,
EQ = FQ (because DQ is the median)
DQ = HQ (by construction)
and \(\angle\) DQE = \(\angle\) HQF (vertically opposite angles)
\(\therefore\) By SAS theorem of congruence,
\(\triangle\) DQE \(\cong\) \(\triangle\) HQF
\(\implies\) DE = HF ………(2) (C.P.C.T)
Now, \(AB\over DE\) = \(AC\over DF\) = \(AP\over DQ\) (given)
From (1) and (2), AB = GC and DE = HF
\(\implies\) \(GC\over HF\) = \(AC\over DF\) = \(AP\over DQ\)
\(\implies\) \(GC\over HF\) = \(AC\over DF\) = \(2AP\over 2DQ\)
\(\implies\) \(GC\over HF\) = \(AC\over DF\) = \(AG\over DH\)
By SSS similarity,
\(\triangle\) AGC ~ \(\triangle\) DHF
\(\implies\) \(\angle\) 1 = \(\angle\) 2
Similarly, \(\angle\) 3 = \(\angle\) 4
Thus, \(\angle\) 1 + \(\angle\) 3 = \(\angle\) 2 + \(\angle\) 4
\(\implies\) \(\angle\) A = \(\angle\) D ……….(3)
Thus, in triangles ABC and DEF,
\(\angle\) A = \(\angle\) D (from 3)
and \(AB\over DE\) = \(AC\over DF\) (given)
So, By SAS similarity,
\(\triangle\) ABC ~ \(\triangle\) DEF
