Solution :
Given : Let AC be a tower casts a shadow BC = 28 m and DF = 6 m be a pole casts a shadow EF = 4m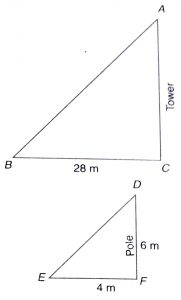
To Find : Height of the tower
Procedure : Now, In triangle ABC and DEF
\(\angle\) ACB = \(\angle\) DEF (each 90)
At the same time the rays of sun have same inclination
\(\implies\) \(\angle\) ABC = \(\angle\) DEF
By AA similarity,
\(\triangle\) ABC ~ \(\triangle\) DEF
\(\implies\) \(AC\over DF\) = \(BC\over EF\)
\(\implies\) \(AC\over 6\) = \(28\over 4\)
\(\implies\) AC = 42 m
Hence, the height of tower is 42 m.
