Solution :
Given : AD and PM are the medians of triangles ABC and PQR respectively, where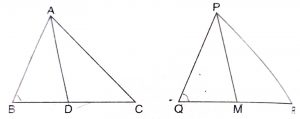 
\(\triangle\) ABC ~ \(\triangle\) PQR.
To Prove : \(AB\over PQ\) = \(AD\over PM\)
Proof : In triangles ABD and PQM, we have
\(\angle\) B = \(\angle\) D (because \(\triangle\) ABC ~ \(\triangle\) PQR)
Since AD and PM are the medians to BC and QR respectively and \(AB\over PQ\) = \(BC\over QR\)
\(AB\over PQ\) = \({1\over2}BC\over {1\over 2}QR\)
So, \(AB\over PQ\) = \(BD\over QM\)
\(\therefore\) By SAS similarity,
\(\triangle\) ABD ~ \(\triangle\) PQM
So, \(AB\over PQ\) = \(BD\over QM\) = \(AD\over PM\)
