Solution :
Let the diagonals BD and AC of the rhombus ABCD intersect each other at O.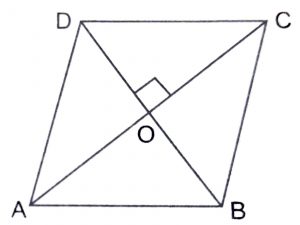
Since the diagonals of the rhombus bisect each other at right angles.
\(\therefore\) \(\angle\) AOB = \(\angle\) BOC = \(\angle\) COD = \(\angle\) DOA = 90
and AO = CO, BO = OD
Since AOB is a right triangle angled at O, therefore,
\({AB}^2\) = \({OA}^2\) + \({OB}^2\)
Since AO = CO, BO = OD,
\(\implies\) \({AB}^2\) = \(({1\over 2}{AB})^2\) + \(({1\over 2}{BD})^2\)
\(\implies\) \(4{AB}^2\) = \({AC}^2\) + \({BD}^2\) ……….(1)
Similarly, we have :
\(4{BC}^2\) = \({AC}^2\) + \({BD}^2\) ……..(2)
\(4{CD}^2\) = \({AC}^2\) + \({BD}^2\) ……..(3)
\(4{AD}^2\) = \({AC}^2\) + \({BD}^2\) ………(4)
Adding all the equations above, we get
\({AB}^2\) + \({BC}^2\) + \({CD}^2\) + \({DA}^2\) = \({AC}^2\) + \({BD}^2\)
