Solution :
Given : \(\triangle\) ABC, in which each side is of length 2a.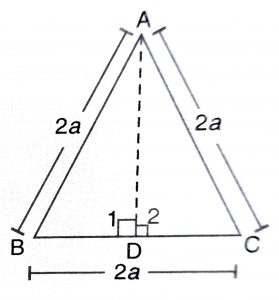
To Find : AD (altitude)
In \(\triangle\) ADB and \(\triangle\) ADC,
AD = AD (common)
\(\angle\) 1 = \(\angle\) 2 (90 each)
AB = AC (given)
By RHS,
\(\triangle\) ADB \(\cong\) \(\triangle\) ADC
So, BD = DC (By C.P.C.T)
\(\implies\) BD = DC = a
Now, in \(\triangle\) ADB,
\({AD}^2\) + \({BD}^2\) = \({AB}^2\)
\(\implies\) \({AD}^2\) + \(a^2\) = \((2a)^2\) (By Pythagoras Theorem)
\({AD}^2\) = \(3a^2\) \(\implies\) AD = \(\sqrt{3} a\)
