Question :
In the figure, O is a point in the interior of a triangle ABC, OD \(\perp\) BC, OE \(\perp\) AC and OF \(\perp\) AB. Show that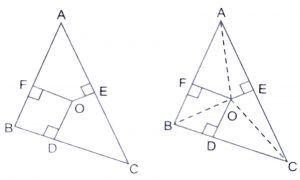
(i) \({OA}^2\) + \({OB}^2\) + \({OC}^2\) – \({OD}^2\) – \({OE}^2\) – \({OF}^2\) = \({AF}^2\) + \({BD}^2\) + \({CE}^2\)
(ii) \({AF}^2\) + \({BD}^2\) + \({CE}^2\) = \({AE}^2\) + \({CD}^2\) + \({BF}^2\)
Solution :
Join AO, BO and CO as shown in fig.
(i) In right \(\triangle\)s OFA, ODB and OEC, we have
\({OA}^2\) = \({AF}^2\) + \({OF}^2\)
\({OB}^2\) = \({BD}^2\) + \({OD}^2\)
and \({OC}^2\) = \({CE}^2\) + \({OE}^2\)
Adding all these, we get
\({OA}^2\) + \({OB}^2\) + \({OC}^2\) = \({AF}^2\) + \({BD}^2\) + \({CE}^2\) + \({OD}^2\) + \({OE}^2\) + \({OF}^2\)
or \({OA}^2\) + \({OB}^2\) + \({OC}^2\) – \({OD}^2\) – \({OE}^2\) – \({OF}^2\) = \({AF}^2\) + \({BD}^2\) + \({CE}^2\)
(ii) In right \(\triangle\)s ODB and ODC, we have :
\({OB}^2\) = \({BD}^2\) + \({OD}^2\) and \({OC}^2\) = \({OD}^2\) + \({CD}^2\)
or \({OB}^2\) – \({OC}^2\) = \({BD}^2\) – \({CD}^2\) ……….(1)
Similarly, we have :
\({OC}^2\) – \({OA}^2\) = \({CE}^2\) – \({AE}^2\) ………..(2)
\({OA}^2\) – \({OB}^2\) = \({AF}^2\) + \({BF}^2\) ………..(3)
Adding equations (1), (2) and (3), we get
\({AF}^2\) + \({BD}^2\) + \({CE}^2\) = \({AE}^2\) + \({CD}^2\) + \({BF}^2\)
