Here you will learn what is the intersection of sets with definition and venn diagram and examples.
Let’s begin –
What is the Intersection of Sets ?
Definition : Let A and B be two sets. The intersection of A and B is the set of all those elements that belong to both A and B.
The intersection of A and B is denoted by \(A \cap B\) (read as “A intersection B”)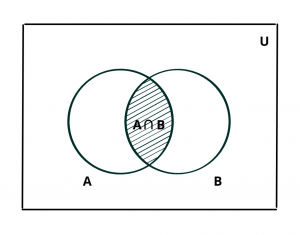
Thus, \(A \cap B\) = {x : x \(\in\) A and x \(\in\) B}.
Clearly, x \(\in\) \(A \cap B\) \(\iff\) x \(\in\) A and x \(\in\) B.
In the given figure, the shaded region represents \(A \cap B\). This is the venn diagram for intersection of sets.
Evidently, \(A \cap B\) \(\subseteq\) A, \(A \cap B\) \(\subseteq\) B.
Note : If \(A_1\), \(A_2\), …. , \(A_n\) is a finite family of sets, then their intersection is denoted by \(A_1 \cap A_2 \cap ….. \cap A_n\).
Example : If A = {1, 2, 3, 4, 5} and B = {1, 3, 9, 12}, then \(A \cap B\) = {1, 3}.
Example : If A = {1, 2, 3, 4, 5, 6, 7}, B = {2, 4, 6, 8} and C = {4, 6, 7, 8, 9, 10, 11}, then find \(A \cap B\) and \(A \cap B \cap C\).
Solution : \(A \cap B\) = {2, 4, 6}
\(\therefore\) \(A \cap B \cap C\) = {4, 6}
Formula to Find Number of Elements in A Intersection B
If A, B and C are finite sets, and U be the finite universal set, then
n(\(A \cap B\)) = n(A) + n(B) – n(\(A \cup B\))
where, n(A) = number of elements in set A
n(B) = number of elements in set B
n(\(A \cup B\)) = number of elements in union of sets A and B
Also Read : Other Formulas and Operation of Sets
Example : If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(\(X \cup Y\)) = 38, then find n(\(X \cap Y\)).
Solution : By using the above formula,
n(\(X \cap Y\)) = n(X) + n(Y) – n(\(X \cup Y\))
\(\implies\) n(\(X \cap Y\)) = 17 + 23 – 38
\(\implies\) n(\(X \cap Y\)) = 2
