Here you will learn what is the union of sets with definition and venn diagram representation and examples.
Let’s begin –
What is the Union of Sets ?
Definition : Let A and B be two sets. The union of A and B is the set of all those elements which belong either to A or to B or to both A and B.
We shall use the notation \(A \cup B\) (read as “A union B”) to denote the union of A and B.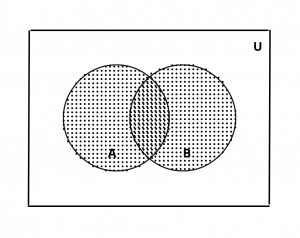
Thus, \(A \cup B\) = {x : x \(\in\) A or x \(\in\) B}.
Clearly, x \(\in\) \(A \cup B\) \(\iff\) x \(\in\) A or x \(\in\) B.
And, x \(\notin\) \(A \cup B\) \(\iff\) x \(\notin\) A or x \(\notin\) B.
In the given figure whole shaded part represents \(A \cup B\). This is the venn diagram for union of sets.
It is evident from the definition the A \(\subseteq\) \(A \cup B\), B\(\subseteq\) \(A \cup B\).
If A and B are two sets such that A \(\subset\) B, then \(A \cup B\) = B. Also, \(A \cup B\) = A, if B\(\subset\) A.
Example : If A = {1, 2, 3} and B = {1, 3, 5, 7}, then \(A \cup B\) = {1, 2, 3, 5, 7}.
Example : If A = {1, 2, 3}, B = {3, 5} and C = {4, 7, 8}. Then \(A \cup B \cup C\) = {1, 2, 3, 4, 5, 7, 8}.
Formula to Find Number of Elements in A Union B
If A, B and C are finite sets, and U be the finite universal set, then
n(\(A \cup B\)) = n(A) + n(B) – n(\(A \cap B\))
where, n(A) = number of elements in set A
n(B) = number of elements in set B
n(\(A \cap B\)) = number of elements in intersection of sets A and B
Also Read : Other Formulas and Operation of Sets
Example : If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(\(X \cap Y\)) = 2, then find n(\(X \cup Y\)).
Solution : By using the above formula,
n(\(X \cup Y\)) = n(X) + n(Y) – n(\(X \cap Y\))
\(\implies\) n(\(X \cup Y\)) = 17 + 23 – 2
\(\implies\) n(\(X \cup Y\)) = 38
