Here you will learn what are disjoint sets in set theory with venn diagram and examples.
Let’s begin –
What are Disjoint Sets ?
Definition : Two set A and B are said to be disjoint, if \(A \cap B\) = \(\phi\).
If \(A \cap B\) \(\ne\) \(\phi\), then A and B are said to be intersecting or overlapping sets.
Also Read : Formulas and Operation of Sets
Venn Diagram of Disjoint Set
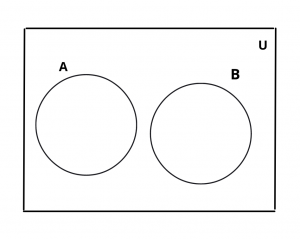
Example : If A = {1, 2, 3, 4, 5, 6}, B = {7, 8, 9, 10, 11} and C = {6, 8, 10, 12, 14}. Then find which of the following two set are disjoint.
Solution : We have sets A, B and C,
Taking intersection of set A and B,
\(A \cap B\) = \(\phi\)
Hence, A and B are Disjoint Sets.
Now, \(A \cap C\) = {6}
Since A intersection C is not \(\phi\). So, they are intersecting sets.
Now, \(B \cap C\) = {8, 10}
Since B intersection C is also not \(\phi\). So, they are also intersecting sets.
