Solution :
(i) In \(\triangle\)s PAC and PDB, we have :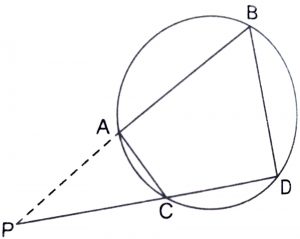
\(\angle\) APC = \(\angle\) DPB (common)
\(\angle\) PAC = \(\angle\) PDB
[\(\therefore\) \(\angle\) BAC = 180 – \(\angle\) PAC and \(\angle\) PDB = \(\angle\) CDB = 180 – (180 – \(\angle\) PAC) = \(\angle\) PAC]
\(\therefore\) By AA similarity, we have :
\(\triangle\) PAC ~ \(\triangle\) PDB
(ii) Since \(\triangle\)s PAC ~ PDB, therefore
\(PA\over PD\) = \(PC\over PB\) or PA.PB = PC.PD.
