In the figure, two chords AB and CD intersect each other at the point P. Prove that (i) \(\triangle\) APC ~ \(\triangle\) DPB (ii) AP.PB = CP.DP

Solution :

(i)  In \(\triangle\)s PAC and PDB, we have :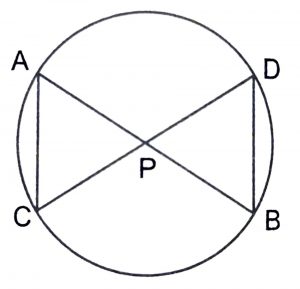

\(\angle\) APC = \(\angle\) DPB         (vertically opp. angles)

\(\angle\) CAP = \(\angle\) BDP        (angles in same segment of circle are equal)

\(\therefore\)  By AA similarity, we have :

\(\triangle\) APC ~ \(\triangle\) DPB 

(ii)  Since \(\triangle\)s APC ~ DPB, therefore

\(AP\over DP\) = \(CP\over PB\)  or  PA.PB = CP.DP.