Solution :
Given : ABC is a triangle and D is point on BC such that \(BD\over CD\) = \(AB\over AC\)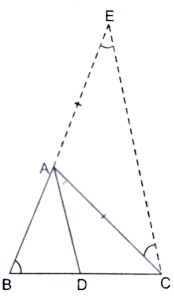
To Prove : AD is the bisector of \(\angle\) BAC.
Construction : Produce line BA to E such that line AE = AC. Join CE.
Proof : In \(\triangle\) AEC, since AE = AC, hence
\(\angle\) AEC = \(\angle\) ACE (angles opposite to equal sides of triangle are equal)
Now, \(BD\over CD\) = \(AB\over AC\) (given)
So, \(BD\over CD\) = \(AB\over AE\) (AE = AC, by construction)
\(\therefore\) By converse of Basic Proportionality theorem(Thales Theorem),
DA || CE
Now, Since CA is a traversal, we have :
\(\angle\) BAD = \(\angle\) AEC ……..(2) [corresponding angles]
and \(\angle\) DAC = \(\angle\) ACE ……..(3) (alternate angles)
Also, \(\angle\) AEC = \(\angle\) ACE (from 1)
From (2) and (3),
\(\angle\) BAD = \(\angle\) DAC
Thus, AD bisects \(\angle\) BAC.
