Solution :
Given : PQR is a triangle and PS is the bisector of \(\angle\) QPR meeting QR at S.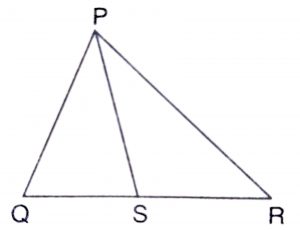
\(\therefore\) \(\angle\) QPS = \(\angle\) SPR
To Prove : \(QS\over SR\) = \(PQ\over PR\)
Construction : Draw RT parallel to SP to cut QP produced at T.
Proof : Since PS || TR and PR cuts them, hence we have :
\(\angle\) SPR = \(\angle\) PRT …….(1) (alternate angles)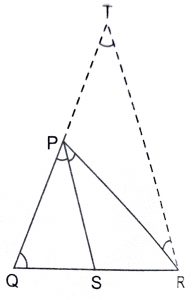
and \(\angle\) QPS = \(\angle\) PTR ………(2) (corresponding angles)
but, \(\angle\) QPS = \(\angle\) PTR ………(3) (given)
\(\therefore\) \(\angle\) PRT = \(\angle\) PTR [From (1) and (2)]
\(\implies\) PT = PR ……….(3) (sides opposite to equal angles are equal)
Now, in \(\triangle\) QRT, we have :
SP || RT (by construction)
\(\therefore\) \(QS\over SR\) = \(PQ\over PT\) (by basic proportionality)
or \(QS\over SR\) = \(PQ\over PR\) (from 3)
