Solution :
We have : AB \(\perp\) BC and DM \(\perp\) BC.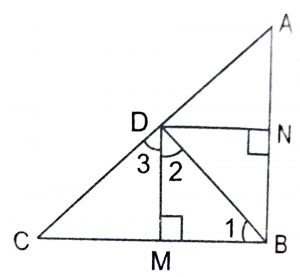
So, AB || DM
Similarly, we have :
BC \(\perp\) AB and DN \(\perp\) AB.
So, CB || DN
Hence, quadrilateral BMDN is a rectangle.
\(\therefore\) BM = DN
(i) In triangle BMD, we have :
\(\angle\)1 + \(\angle\) BMD + \(\angle\)2 = 180
or \(\angle\)1 + 90 + \(\angle\)2 = 180
\(\implies\) \(\angle\)1 + \(\angle\)2 = 90
Similarly, in triangle BMC, we have :
\(\angle\)3 + \(\angle\)4 = 90
Since BD \(\perp\) AC, therefore
\(\angle\)2 + \(\angle\)3 = 90
Now, \(\angle\)1 + \(\angle\)2 = 90 and \(\angle\)2 + \(\angle\)3 = 90
\(\therefore\) \(\angle\)1 + \(\angle\)2 = \(\angle\)2 + \(\angle\)3
So, \(\angle\)1 = \(\angle\)3
Also, \(\angle\)3 + \(\angle\)4 = \(\angle\)2 + \(\angle\)3 \(\implies\) \(\angle\)2 = \(\angle\)4
Thus, in triangles BMD and BMC, we have :
\(\angle\)1 = \(\angle\)3 and \(\angle\)2 = \(\angle\)4
\(\therefore\) By AA similarity, we have :
\(\triangle\) BMD ~ \(\triangle\) DMC
So, \(BM\over DM\) = \(MD\over MC\)
Since, BM = ND,
\(\implies\) \(DN\over DM\) = \(DM\over MC\)
So, \({DM}^2\) = DN.MC
(ii) Proceeding as in (i), we can prove that
\(\triangle\) BND ~ \(\triangle\) AND
So, \(BN\over DN\) = \(ND\over NA\)
Since, BN = DM,
\(\implies\) \(DM\over DN\) = \(DN\over AN\)
So, \({DN}^2\) = DN.MC
