Solution :
Given : ABC is triangle in which \(\angle\) ABC > 90 and AD \(\perp\) CB produced.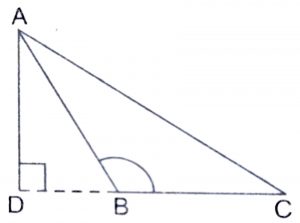
To Prove : \({AC}^2\) = \({AB}^2\) + \({BC}^2\) + 2BC.BD
Proof : Since \(\triangle\) ADB is a right triangle, angled at D. Therefore, by Pythagoras theorem,
\({AB}^2\) = \({AD}^2\) + \({DB}^2\) ……..(1)
Again, in triangle ADC is a right triangle, angled at D.
Therefore, by Pythagoras theorem, we have :
\({AC}^2\) = \({AD}^2\) + \({DC}^2\)
\(\implies\) \({AC}^2\) = \({AD}^2\) + \({DB + BC}^2\)
\(\implies\) \({AC}^2\) = \({AD}^2\) + \({DB}^2\) + \({BC}^2\) + 2BC.BD
\(\implies\) \({AC}^2\) = \({AB}^2\) + \({BC}^2\) + 2BC.BD (by using 1)
