Solution :
Consider a triangle ABC in which \(\angle\) B = 90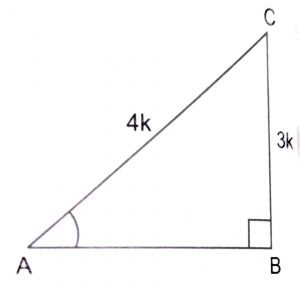
For \(\angle\) A, we have :
Base = AB, Perpendicular = BC and Hypotenuse = AC,
\(\therefore\) Sin A = \(perpendicular\over hypotenuse\) = \(BC\over AC\) = \(3\over 4\)
Let BC = 3k and AC = 4k,
Then, \({AB}^2\) = \({AC}^2 – {BC}^2\) = \(\sqrt{7}\)
\(\therefore\) cos A = \(Base\over Hypotenuse\) = \(AB\over AC\) = \(\sqrt{7}\over 4\)
and tan A = \(perpendicular\over hypotenuse\) = \(BC\over AB\) = \(3\over \sqrt{7}\)
