Solution :
In triangle PQR, we have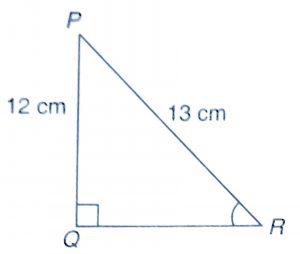
\(\angle\) Q = 90, PQ = 12 cm and PR = 13 cm
Using Pythagoras Theorem,
\({PR}^2\) = \({PQ}^2\) + \({QR}^2\)
\(\implies\) \({QR}^2\) = \({PR}^2\) – \({PQ}^2\)
= \((13)^2\) – \((12)^2\) = 25
\(\implies\) QR = 5 cm
We know that,
tan P = \(QR\over PQ\) = tan P = \(5\over 12\) ……..(1)
cot R = \(QR\over PQ\) \(\implies\) cot R = \(5\over 12\) ………(2)
From (1) and (2), we have
tan P – cot R = \(5\over 12\) – \(5\over 12\) = 0
