Solution :
We have,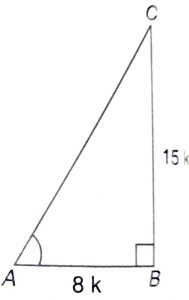
15 cot A = 8 \(\implies\) cot A = \(8\over 15\)
Draw a right triangle ABC,
cot A = \(AB\over BC\) = \(8\over 15\)
If BC = 15k, then AB = 8k, where k is any positive number.
By using Pythagoras Theorem,
\({AC}^2\) = \({AB}^2\) + \({BC}^2\)
= \(64k^2\) + \(225k^2\) = \(289k^2\)
\(\implies\) AC = 17k
Thus, sin A = \(BC\over AC\) = \(15k\over 17k\) = \(15\over 17\)
sec A = \(AC\over AB\) = \(!7k\over 8k\) = \(17\over 8\)
