Solution :
Consider a triangle ABC in which \(\angle\) A = \(\theta\) and \(\angle\) B = 90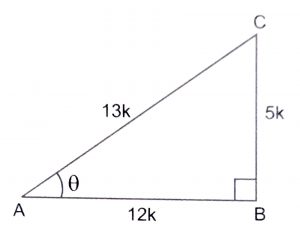
Then, Base = AB, perp = BC and Hypo. = AC,
\(\therefore\) \(sec \theta\) = \(perp\over hypo\) = \(BC\over AC\) = \(3\over 4\)
Let AC = 13k and AB = 12k. Then,
By using Pythagoras Theorem,
\({BC}^2\) = \({AC}^2\) – \({AB}^2\)
= \(169k^2\) – \(125k^2\) = \(25k^2\)
\(\implies\) BC = 5k
\(sin \theta\) = \(BC\over AC\) = \(5\over 13\)
\(cos \theta\) = \(AB\over AC\) = \(12\over 13\)
\(tan \theta\) = \(BC\over AB\) = \(5\over 12\)
\(cot \theta\) = \(AB\over BC\) = \(12\over 5\)
\(cosec \theta\) = \(AC\over BC\) = \(13\over 5\)
