Solution :
Let us consider two right triangles PQA and RSB in which cos A = cos B (see figure).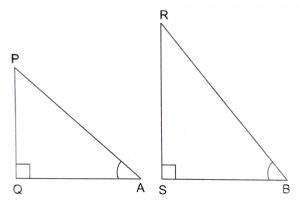
We have : cos A = \(QA\over PA\)
and cos B = \(SB\over RB\)
Thus, it is given that
\(QA\over PA\) = \(SB\over RB\)
So, \(QA\over SB\) = \(PA\over RB\) = k (say)
Now, By Pythagoras Theorem,
PQ = \(\sqrt{{PA}^2 – {QA}^2}\)
and RS = \(\sqrt{{RB}^2 – {SB}^2}\)
So, \(PQ\over RS\) = \(\sqrt{{PA}^2 – {QA}^2}\over \sqrt{{RB}^2 – {SB}^2}\)
or \(PQ\over RS\) = \(k\sqrt{{PA}^2 – {QA}^2}\over \sqrt{{RB}^2 – {SB}^2}\) = k
Therefore, from (1) and (2), we have :
\(QA\over SB\) = \(PA\over RB\) = \(PQ\over RS\)
By SSS similarity,
\(\triangle\) PQA ~ \(\triangle\) RSB
Therefore, \(\angle\) A = \(\angle\) B (Corresponding Angles)
