If cot \(\theta\) = \(7\over 8\), evaluate : (i) \({(1 + sin\theta)(1 – sin\theta)}\over {(1 + cos\theta)(1 – cos\theta)}\) (ii) \(cot^2 \theta\)

Solution :

(i)  In \(\triangle\) ABC,  \(cot \theta\) = \(7\over 8\) = \(AB\over BC\)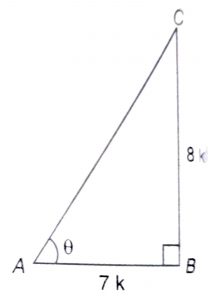

Let AB = 7k and BC = 8k

Now, AC = \(\sqrt{{AB}^2 + {BC}^2}\) = \(\sqrt{113k^2}\)

So, AC = \(\sqrt{113}k\)

Thus,  \(sin \theta\) = \(8k\over \sqrt{113}k\) = \(8\over \sqrt{113}\)

\(cos \theta\) = \(7k\over \sqrt{113}k\) = \(7\over \sqrt{113}\)

Now,  \({(1 + sin\theta)(1 – sin\theta)}\over {(1 + cos\theta)(1 – cos\theta)}\) = \(49\over 64\)

(ii)  \(cot^2 \theta\) = \(({7\over 8})^2\) = \(49\over 64\)