Solution :
Let AB = 24 m be guy wire attached to a vertical pole BC of height 18 m. To keep the wire taut, let it be fixed to stake at A. Then, ABC is a right angled triangle at C.
\(\therefore\) \({AB}^2\) = \({AC}^2\) + \({BC}^2\)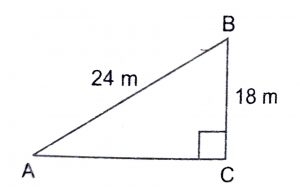
So, \({24}^2\) = \({AC}^2\) + \({18}^2\)
\(\implies\) \({AC}^2\) = 576 – 324
\(\implies\) \({AC}^2\) = 252
\(\implies\) AC = \(6\sqrt{7}\)
Hence, the stake may be placed at a distance of \(6\sqrt{7}\) m from the base of pole.
