Solution :
Let the first plane starts from O and goes upto A towards north.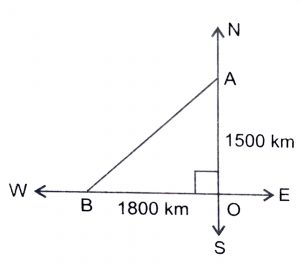
Where OA = (\(1000 \times {3\over 2}\)) km = 1500 km
Let the second plane starts from O at the same time and goes upto B towards west, where OB = (\(1200 \times {3\over 2}\)) km = 1800 km
According to the question, the required distance = BA.
In right triangle ABC, by Pythagoras theorem, we have :
\({AB}^2\) = \({OA}^2\) + \({OB}^2\)
= \((1500)^2\) + \((1800)^2\)
= 2250000 + 3240000
= 5490000
AB = \(3\times 100\sqrt{61}\) = \(300\sqrt{61}\).
