What is the Value of Cosec 45 Degrees ?

Solution :

The value of cosec 45 degrees is $\sqrt{2}$.

Proof :

Let ABC be a triangle, right angled at B, in which $\angle$ A = $\angle$ C = 45 degrees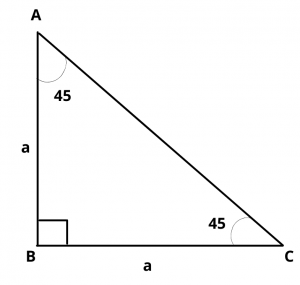

$\therefore$  BC = AB

Let  AB = BC = a

Then by pythagoras theorem,

$AC^2$ = $AB^2$ + $BC^2$ = $a^2$ + $a^2$ = $2a^2$

$\implies$  AC = $\sqrt{2}a$

In $\Delta$ ABC,  $\angle$ C = 45 degrees

By using trigonometric formulas,

$cosec 45^{\circ}$ = $hypotenuse\over perpendicular$ = $h\over p$

$cosec 45^{\circ}$  = hypotenuse/side opposite to 45 degrees = $AC\over AB$ = $\sqrt{2}a\over a$ = $\sqrt{2}$

Hence, the value of $cosec 45^{\circ}$ = $\sqrt{2}$